Las medias (III)

Visto que hay diversas medias, y que dan resultados distintos para un mismo conjunto de datos, seguro que algún estudiante habrá pensado "¿Sacaría mejores notas si el profesor usara otra media?¿Depende de los datos?"

Se puede demostrar por inducción que la media aritmética es siempre mayor o igual que la media geométrica; pero para no perder aún más lectores, aquí lo haremos de una manera más "simpática" (limitándonos, eso sí, a un conjunto de dos números).

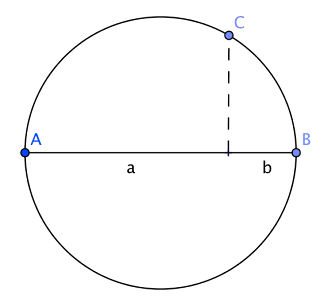
Sean \(a\) y \(b\) dos números cualesquiera. Construimos un segmento de longitud \(a + b\) y lo usamos como diámetro de una circunferencia.

Sean \(A\) y \(B\) los puntos en los que dicho segmento corta a la circunferencia.



Ahora levantamos una perpendicular al diámetro que pase por el punto en el que se unen los segmentos \(a\) y \(b\). Llamamos \(C\) al punto en el que dicha perpendicular corta la circunferencia.

De acuerdo con el segundo teorema de Tales, el triángulo \(ABC\) es rectángulo.

Los triángulos \(AC'C\) y \(BCC'\) son semejantes, ya que sus tres ángulos son iguales (se ve más claramente si rotamos el segundo 90 grados en sentido antihorario).

Sea \(h\) la longitud del segmento \(CC'\).

 Puesto que ambos triángulos son semejantes, se verifica que $$\frac{h}{b}=\frac{a}{h}$$ De donde despejando \(h\), se obtiene $$h^2=ab$$ es decir,  que el segmento \(CC'\) es la media geométrica de las longitudes de los dos segmentos iniciales $$h=\sqrt{ab}$$

Conclusión

Puesto que el radio de la circunferencia es la media aritmética de dichas longitudes (recordemos que el diámetro mide \(a+b\)),

se puede comprobar que la media aritmética de dos números cualesquiera es siempre mayor o igual que su media geométrica. $$\bar{x} \ge G$$

Será igual únicamente en el caso de que \(a=b\), en cuyo caso el segmento \(CC'\) coincidirá con el radio.

En la próxima entrada haremos un cálculo equivalente con la media armónica y la cuadrática. Mientras tanto, ¡seguid dudando!