En numerosas ocasiones habremos leído sobre un concepto llamado ‘ESI’ o ‘IST’, en castellano, al que se suele citar con relativa frecuencia en textos científicos referentes al ámbito de la exoplanetología, pero del que no se explica absolutamente nada, o de forma muy vaga, y ya no hablemos de su cálculo.
La publicación de hoy tiene como fin explicar las aplicaciones que tiene este valor, enseñar a los lectores a calcularlo, comparar los valores de numerosos cuerpos del Sistema Solar con la Tierra y los exoplanetas más potencialmente habitables, así como también introducir los distintos tipos de exoplanetas que existen según sus características físicas.
El Índice de Similitud Terrestre, al que se cita muy frecuentemente como ‘EST’ por sus siglas en inglés (Earth Similarity Index) es un valor que nos permite conocer el grado de similitud entre la Tierra y cualquier objeto del Universo desde 0 (ninguno) hasta 1 (igual a la Tierra). Este índice, pese a que es complicado de hallar en el caso de los exoplanetas (porque las mediciones que podemos realizar desde la Tierra son muy variables y, en cierto modo, imprecisas), es uno de los más utilizados orientativamente para conocer las características físicas y la posible y/o potencial habitabilidad del cuerpo.
Para el cálculo del IST se tienen en cuenta cuatro variables: el radio del cuerpo (en unidades terrestres, 6371 kilómetros equivalen a 1), la velocidad de escape (en unidades terrestres también, 11’19 kilómetros por segundo equivalen a 1), la temperatura superficial (ahora sí, en Kelvin, siendo 288K el valor de referencia para la Tierra) y la densidad del cuerpo (en unidades terrestres, siendo 5514 kg por metro cúbico el equivalente a 1).
En la fórmula, simplemente hay que sustituir. La variable X(i) hace referencia al valor (en Kelvin si hablamos de temperatura o en unidades terrestres si hablamos de radio, densidad o velocidad de escape) del planeta. X(i0) hace referencia al valor de la Tierra para ese apartado (1 en todos los aspectos menos en la temperatura, donde colocaremos 288). Lo mismo en el denominador.
Después, el resultado de la fórmula debemos elevarlo al cociente entre w(i) y n, siendo w(i) el peso que tiene en la fórmula el parámetro que estamos calculando y siendo ‘n’ el número de parámetros que estamos calculando, siempre 1, ya que los vamos a calcular siempre individualmente. Tras tener los cuatro valores calculados, los sumaremos y dividiremos entre cuatro para así calcular su promedio, que no será sino el IST.
El peso de cada apartado (el valor de W(i)) es de 5.58 para la temperatura, 0.7 para la velocidad de escape, 1.07 para la densidad y 0.57 para el radio.
Solo hay que tener especial cuidado con una cuestión: el valor absoluto del cociente. Este quiere decir que, sea cual sea el resultado del mismo (positivo o negativo), adoptará siempre el valor positivo. Por ejemplo, si el resultado del cociente fuese -1, el valor absoluto lo convertiría en +1. Así, en lugar de calcular 1-(-1), que sería 2, se calcula 1-(+1), que es 0. SIEMPRE que apliquemos la fórmula, deberemos restar un valor positivo. Si no, algo habremos realizado mal y deberemos revisar la fórmula de nuevo para corregir nuestro error.
Así pues, vamos a poner toda la teoría en práctica con Marte:
Para el caso de Marte, vamos a ir a la página web más fiable existente a nivel de datos planetarios de todo Internet: la NASA Fact Sheet u ‘Hoja de Datos de la NASA’. De entre las decenas de variables que nos permiten conocer, nos quedaremos con las cuatro seleccionadas, que son:
- Radio: 0.531 unidades terrestres.
- Densidad: 0.713 unidades terrestres.
- Temperatura Atmosférica: 210K
- Velocidad de escape: 0.450 unidades terrestres.
Sustituimos en la fórmula:
- Para el radio, el IST es de: (1-0.3063357283)0.57 = 0.8118113442.
- Para la densidad, el IST es de: (1-0.1675423234)1.07 = 0.8218404519.
- Para la velocidad de escape, el IST es de: (1-0,3793103448)0.7 = 0,7161634539.
- Para la temperatura, el IST es de: (1-0.156626506)5’58 = 0’3865372102.
Para calcular el IST, sumaremos los cuatro valores y los dividiremos entre cuatro. El IST de Marte es de 0,6840881151 (0.684), o un 68,4% de parecido con la Tierra.
Este índice, que va desde 0 hasta 1, ha sido ampliamente utilizado por los astrónomos para clasificar a los exoplanetas. Valores de 0 a 0.6 corresponden a cuerpos inhóspitos o potencialmente inhóspitos (al menos según todo lo que conocemos sobre la vida a día de hoy). Dentro de este colectivo se encuentran, por ejemplo, la Luna (0.56), Mercurio (0.39), Plutón (0.08)…
Valores entre 0.6 y 0.7 corresponden a cuerpos en los que la posibilidad de hallar vida es muy complicada y, en algunos, hasta imposible. Se situarían dentro del 0.7 todos los cuerpos que reúnen algunas de las condiciones físicas y/o químicas para albergar vida y una atmósfera y, a partir de 0.8 se situarían los planetas rocosos de volumen y radio similares al terrestre en los que podría haber una atmósfera y, por ende, vida en cualquiera de sus formas. Son pocos los exoplanetas confirmados que posean un IST de 0.8 o superior, aunque sí que hay muchos bastante similares a la Tierra que están siendo objeto de estudio, que son –por orden y junto a su año de descubrimiento-:
Kepler 438b es el exoplaneta más parecido a la Tierra
descubierto hasta la fecha.
1. Kepler-438b, (2015), 0.88.
2. Kepler-296e (2014), 0.85.
4. Kepler-442b, (2015), 0.84.
Estos seis cuerpos, dos de ellos descubiertos este año, son las gemas de la exoplanetología, todavía algunos de ellos muy desconocidos, y otros siempre presentes en la lista año tras año. Y remarco esto porque es un gran problema del IST y en general de esta ciencia: la imprecisión y la grandísima variabilidad de los cálculos.
El IST, en definitiva, es un índice meramente orientativo, que puede indicar el grado en que la Tierra se parece a cualquier otro cuerpo del Universo, pero jamás debe ser tomado como la certeza de que por ser alto debe de haber vida, atmósfera, civilización inteligente, océanos o miles de realidades más que muchos pretenden relacionar con él. Dos planetas pueden tener un mismo índice siendo radicalmente distintos, o incluso uno similar al de la Tierra siendo potencialmente inhóspitos. El IST es quizá una de las mejores herramientas de la exoplanetología para comparar, pero jamás para afirmar.

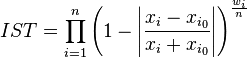














Gran artículo! no tenía idea de este índice y aprendí bastante del tema.
ResponderEliminar